A Brief Guide to Human-Sized Numbers
One of the things that makes climate science confusing is the huge numbers thrown around. Numbers like Gigatons, Terawatts, or Exajoules. It’s hard for numbers this large to feel real to us.
One way to tackle this problem is to divide a very large number by another large number, to end up with a human-sized number. This is like how the size of an economy is easier to understand when expressed per capita.
For example, the total energy that the Earth absorbs from the sun each day is an unrelatably massive number — 10 Zettajoules. (A Zettajoule is 10^21 Joules, or a thousand billion billion Joules. By comparison, annual human energy consumption is about half a Zettajoule.)
This is an unwieldy number. However, if we divide this by the surface area of the Earth, and by the number of seconds in a day, we find that on average, every square meter of the Earth receives about 240 Joules of solar energy per second (these numbers are all after taking into account that our planet reflects away 30% of sunlight).
The term ‘heat flux’ (or energy flux) tells you how much energy is received or emitted by one square meter of surface area in one second. The more intense the energy flow, the higher the heat flux.

So Earth’s incoming solar flux, averaged over the entire planet, is roughly 240 Joules / second / square meter, or 240 Watts / square meter (240 W/m², for short).
How does this number compare to everyday things? If I sat on the ground, I’d be warming the patch of Earth underneath me with a heat flux of about 50 W/m². If I placed my laptop on the ground while it was running, it would heat the Earth under it with an intensity of 100 W/m².
So measuring things this way puts climate-sized numbers and human-sized numbers in the same ballpark.
Worth remembering: The Earth receives energy at a rate of ~240 W/m² from the Sun. That’s our incoming solar flux.
(If you’ve taken some physics, you might have heard that the solar constant is ~ 1360 W/m². That’s the maximum solar flux at the equator, facing the sun, without any clouds. To take into account day and night, and the variation across Earth’s curved surface, we divide this number by 4. Also, Earth reflects away 30% of incoming light, so we multiply this number by 70% — the fraction of sunlight absorbed by the planet. All together, 1360 * 0.7 / 4 ≈ 240)
Where does the energy go?
As the Earth absorbs the sunlight raining down on it, its atoms and molecules start to jiggle. We call this collective jiggling temperature.
Quantum mechanics teaches us that when atoms and molecules jiggle, they emit photons. Each of these photons carries away a tiny bit of energy (a quantum of energy).
This is how stuff gets rid of excess energy. The hotter an object, the more heat it sheds in the form of photons. This is why when you look at things with an infrared camera, hotter objects glow more brightly than cold ones.

Image: Infrared Dog. NASA/IPAC
There’s a straightforward equation connecting the temperature of an object to its heat glow. Using this relationship, an infrared thermometer can tell you something’s temperature, just by looking at its invisible glow.
(Fun fact: if you point an infrared thermometer at the sky, the temperature it displays measures the greenhouse effect.)
Here’s that equation:

T represents the temperature, measured in Kelvin. The symbol σ is a conversion factor between temperature and heat flux, known as the Stefan-Boltzmann constant.

With this equation in hand, you can work out how much heat is radiated by an object at any temperature. Just plug in a temperature, and it’ll spit out a heat flux.
Let’s take a stab at using this equation to predict planetary temperatures. Spoiler alert: we’ll get it wrong, but we’ll learn something interesting.
Predicting Planetary Temperatures
Imagine that we created Earth from scratch, as a frozen, lifeless rock that’s as cold as the background temperature of outer space. We gently place this planet into Earth’s orbit. All of a sudden, sunlight starts streaming in. As a result of all this energy pouring in, Earth’s temperature rises.
Here’s an animation depicting this process (you might recognize this cartoon model from the previous newsletter.)
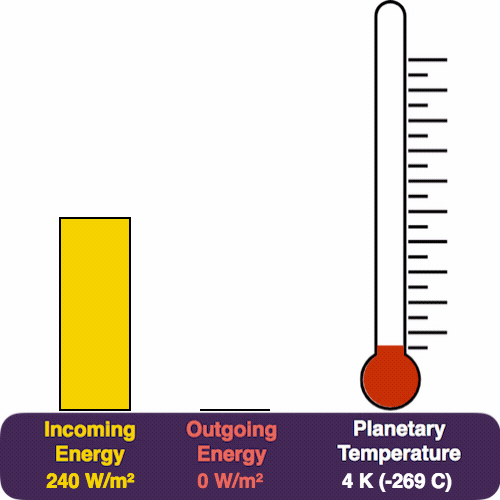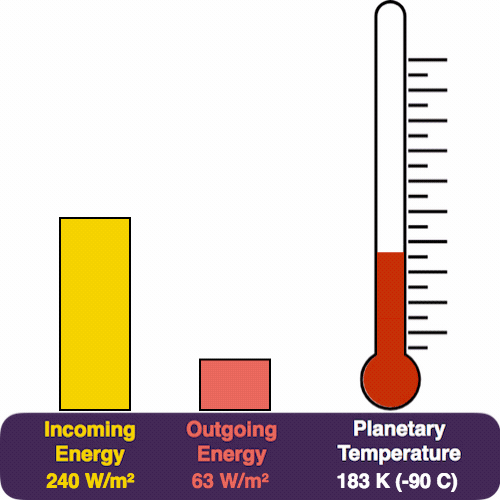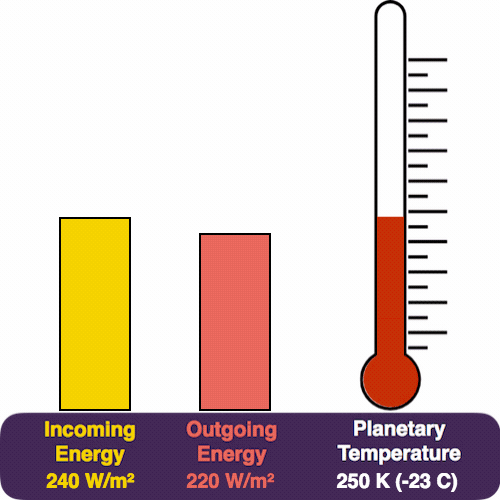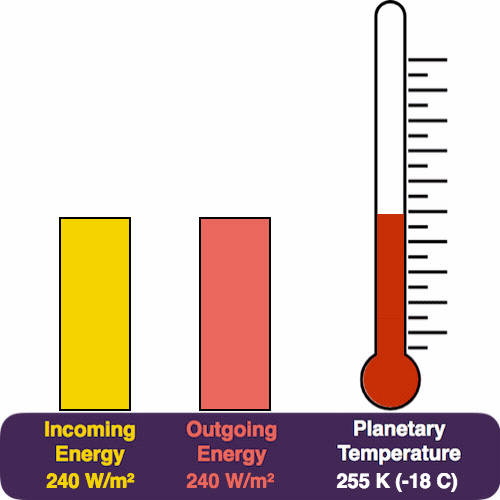
The yellow pile represents the energy coming in from the Sun, which pours in at a rate of 240 W/m². The red pile is the heat that we radiate (measured in the same units). The thermometer measures our temperature.
In the previous newsletter, we saw how any energy imbalance (energy in minus energy out) causes the temperature to change. Since the yellow pile exceeds the red, the planet warms up.
As the temperature rises, so does Earth’s heat glow. And so the red pile also starts to grow.
Eventually we reach a trade-off, where the two piles balance each other, and the temperature stabilizes. So this feedback mechanism automatically adjusts Earth’s temperature in response to the incoming energy, a bit like how a thermostat maintains a temperature.
The Kitchen Sink Analogy
This balancing process can be a little hard to think about. So here’s an analogy to help, that comes to us from the French physicist Joseph Fourier. In his classic 1827 paper that described for the first time how Earth maintains its temperature, Fourier writes that you can think about Earth’s heat flow as “analogous to [..] a vessel which receives, through its upper opening, a liquid [..], and which allows liquid to escape at a precisely equal rate through one or more openings.”
Fourier was imagining something like a bathtub or a kitchen sink, with water pouring in from a faucet above, and a drain from which water flows out.
Here’s an animation of this process, created by my amazing colleague Shefali Nayak.
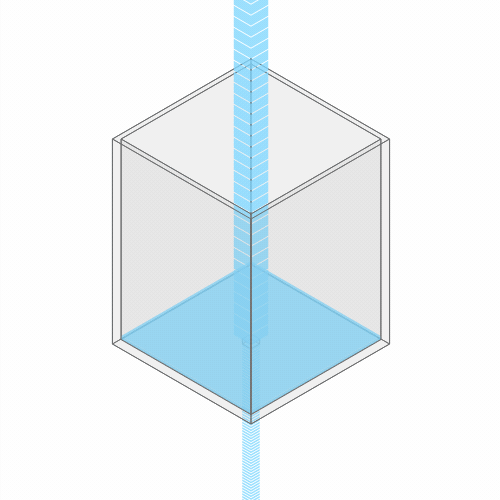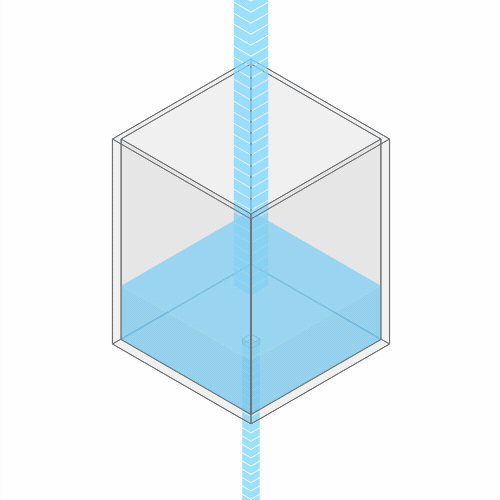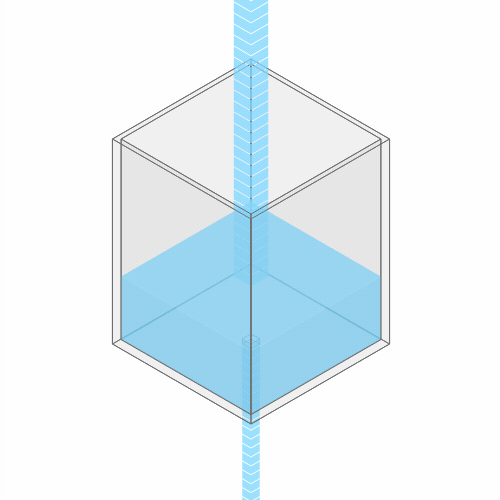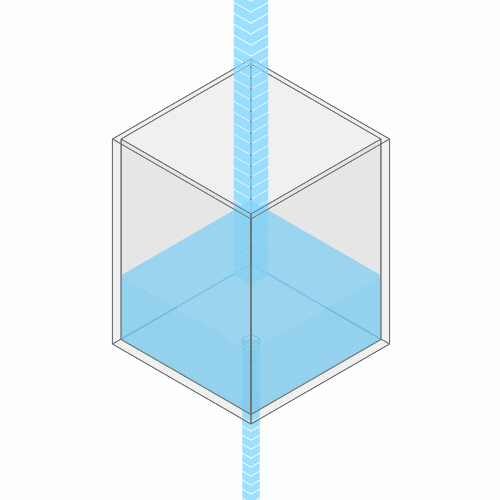
In a leaky sink or bathtub with water pouring in, the water level finds a stable balance
At first, there’s more water flowing into the bathtub than flowing out. So, the water level rises. But as the water rises, the added weight of all this water pushes down more forcefully. So the outflow increases.
Eventually, the water level reaches a balance, where the flow coming in from the faucet exactly balances the flow going down the drain. (You can see this effect for yourself by punching a hole in a paper cup and placing it under a stream of water.)
What happens if you turn up the faucet?
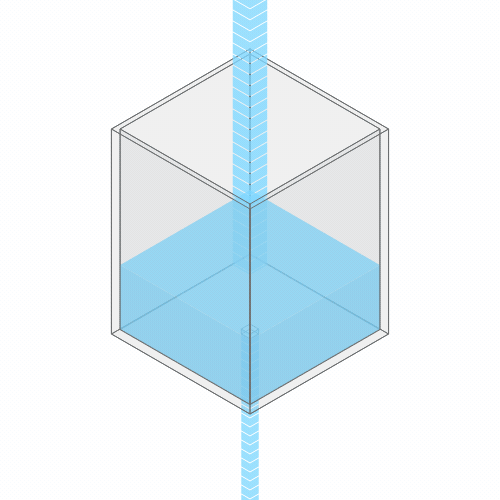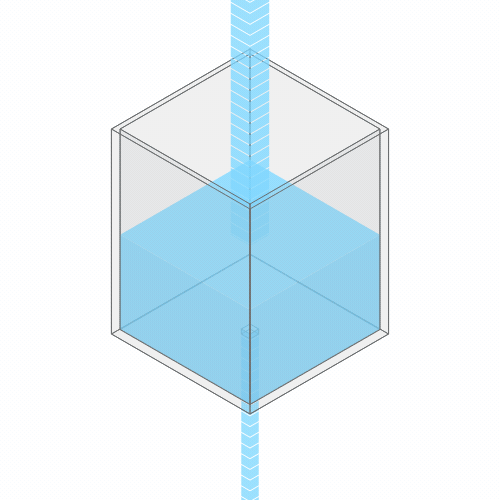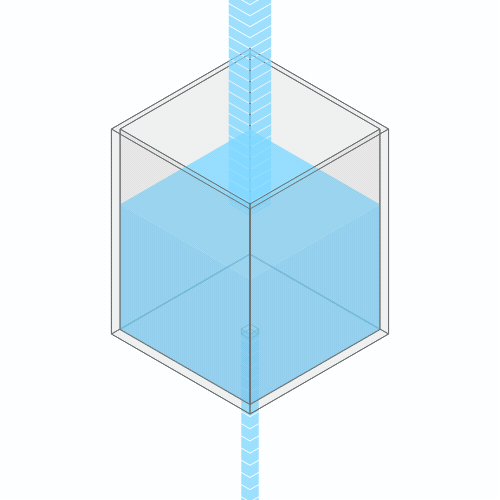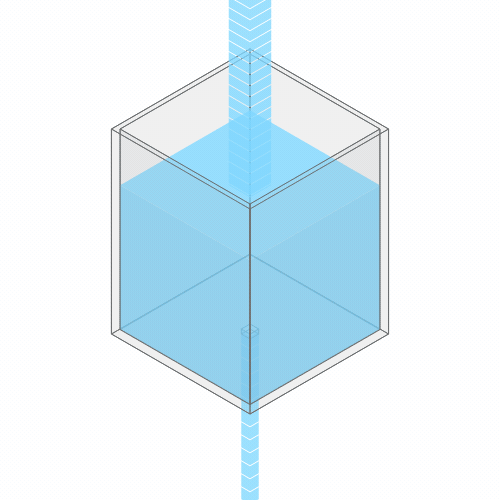
Turning up the faucet raises the water level to a new stable balance.
If you turn up the faucet to increase the incoming water flow, the water level rises, until it reaches a new balance where the flow out once again matches the flow in.
It’s the same idea with Earth’s energy balance. The incoming solar energy is like the water pouring in, and the heat that we emit to space is like the water flowing down the drain. Our temperature is like the water level in this analogy. Just as the water level adjusts itself in response to the incoming flow, Earth’s temperature does the same thing in response to our incoming energy flow.
A Look at the Numbers
We can express this balance as a simple equation:

We know that Earth’s incoming energy flow is 240 W/m². The outgoing energy flow — the heat that we radiate into outer space — is determined by the T⁴ law that we encountered earlier.
So,

Solving for the temperature, we arrive at a planetary temperature of 255 Kelvin, or about -18C (0F).
(Notice that we didn’t mention how big the planet is. That’s because the planet’s size cancels out. A bigger planet will absorb more sunlight, but it will also radiate more heat. Both quantities grow in proportion to surface area. So, as long as we’re measuring heat flow per square meter of surface, we don’t need to worry about the planet’s size.)
That’s way too cold — about 33 C colder than Earth’s actual average temperature. The reason we were off by so much is that we didn’t account for the greenhouse effect. Without the warming influence of the atmosphere, Earth would be completely frozen over, like a giant snowball. (As it turns out, this calculation correctly tells us the temperature at the top of our atmosphere, above the region where the greenhouse effect acts.)
So this model is clearly wrong (or rather, it’s incomplete). But it’s still useful.
To see why, let’s think about the four planets closest to the Sun. Here’s the solar flux (the incoming energy flow) absorbed by the four innermost planets, after accounting for each planet’s albedo.

To get these numbers, I looked up the solar irradiance of each planet in NASA’s Planetary Fact Sheet. To convert that to the average solar flux absorbed by the planet, multiply by (1 - Bond albedo) and divide by 4.
Notice that Venus is an outlier. It’s closer to the Sun than we are, so you’d expect its solar flux to be higher than ours. The reason this value is so low is that Venus is mostly blanketed by clouds, and so 77% of the light that strikes Venus bounces off.
Now that we have the incoming energy flow for each planet, we can try to predict its temperature.
Here, try it yourself, by playing with this little interactive website.
So what do we find? The image below compares the predicted temperatures for each planet, based on our very simple heat radiation model, to the actual temperatures observed on these planets (which you can find here).

This is pretty interesting.
We get surprisingly close to the observed temperatures of Mercury and Mars. (The exact values will differ a bit based on what references you use, but the trend is clear.)
However, when it comes to Earth and Venus, we’re way off. For Venus, our prediction is spectacularly wrong!
You already know why this is — the greenhouse effect. Our model assumed no atmosphere or greenhouse gases. Turns out, this is a pretty good assumption for Mercury and Mars, so we more or less nailed those predictions. But when it comes to the Earth, and especially Venus, neglecting the warming effect of the atmosphere means that this simple model is way off in its predictions.
The last row of the image is the difference between the actual planetary temperature and our predicted temperature (also sometimes called the planetary equilibrium temperature, or the planet’s blackbody temperature). This temperature difference measures the strength of the greenhouse effect on each planet.
Adding in the Greenhouse Effect
Let’s do one last thing. We’ve seen how we can model Earth’s temperatures by ignoring the greenhouse effect. Doing this, we get the wrong temperature.
What if we fiddle with our simple model, and try to work out how much incoming energy it would take to heat the Earth up to our actual temperature?
I encourage you to try this out for yourself. Set the slider in this interactive to Earth’s solar flux. Then, slowly move the slider to the right, until the temperature hits 15° C, the average temperature on our planet. (If you overshoot you can always step back.)
If you do that, you’ll discover something like this:

The picture on the left is what things look like at the top of our atmosphere, where it’s cold, and we’re above the effect of the greenhouse gases.
The picture on the right is what things look like on Earth’s surface.
According to the picture on the right, Earth’s surface emits 390 W/m² of infrared heat.
According to the picture on the left, at the top of the atmosphere, only 240 W/m² of infrared heat makes it out to space.
Together these pictures teach us that out of the 390 W/m² of infrared heat that Earth’s surface emits, only 240 W/m², or about 60%, makes it all the way out to space. The remaining 150 W/m², or 40%, is absorbed by greenhouse gases and sent back down to us, adding to our yellow pile.
So this is how the greenhouse effect works. Part of the heat that we radiate is sent back down to us, similar to how those emergency reflective blankets keep people warm. The difference between the piles on the left and the right picture is 150 W/m² — this number is another way that scientists quantify the strength of our greenhouse effect.
Going back to the water analogy, this is somewhat analogous to when the drain in your bathtub is partially clogged with hair (ugh), and so the water level in your bathtub rises to a higher level.
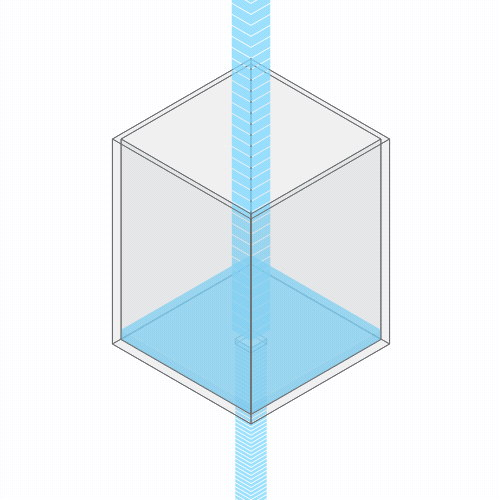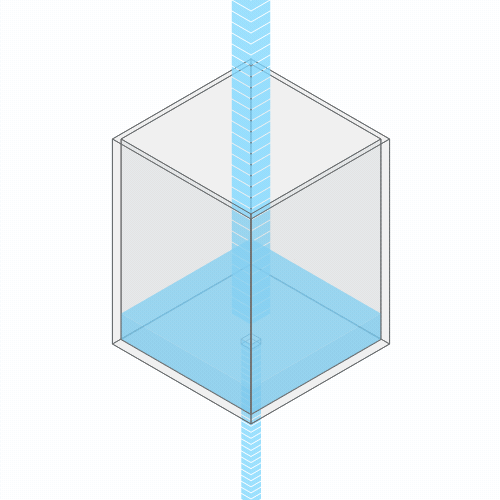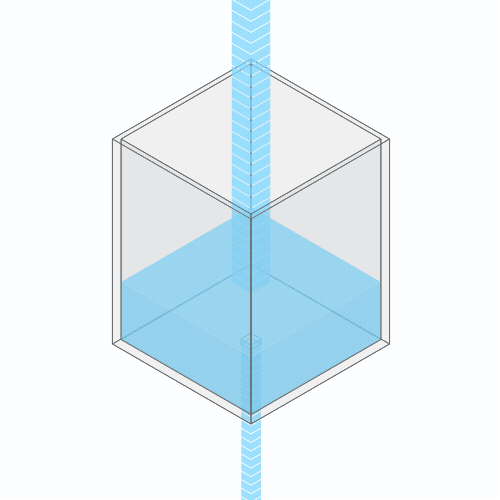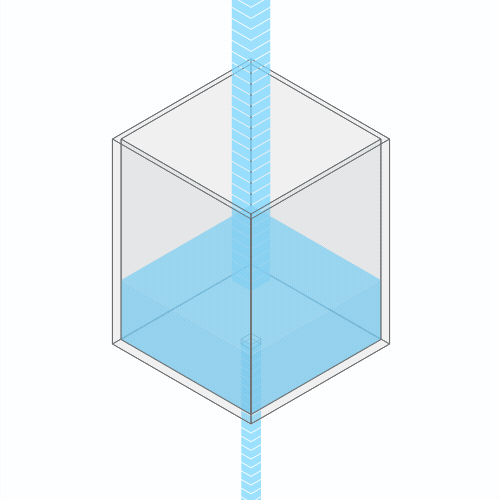
If you clog the drain, the water level rises, until it settles into a new equilibrium.
Greenhouse gases are clogging Earth’s heat drain. Just as every hair that you shed in the bathtub adds to the cumulative clogging of your shower drain, and causes an incremental rise in water level, every unit of CO2 that we emit has a similar effect on Earth’s temperature.
Historically, our partially clogged heat drain wasn’t a bad thing. It kept our planet at a comfortable, habitable temperature, instead of being frozen over. But what we need to worry about today is the very sudden, massive surge in this clogging, from all the greenhouse gases we’ve added over the last century.
So the next time the you find yourself cleaning a clogged shower drain, you can think about how your situation is a metaphor for our planet’s fate.
Welcome to all the new subscribers, including all the folks arriving from the Dear Hank & John podcast. Hi! 👋🏽👋🏽 Thanks for subscribing, and feel free to reply to this email to introduce yourself, or to share your feedback & ideas. I’d love to hear what you think. If you find this newsletter valuable, consider sharing it with a friend. It really helps get the word out!
Last Week in Climate News
One of the biggest recent climate stories was the publication of the new UN special report issued on Climate Change and Land.
Robinson Meyer at the Atlantic did a spectacular job of covering this story, and driving home the magnitude of the stakes involved.
Christoper Flavelle covered the story in NYT.
Here’s Carolyn Kormann’s writeup in The New Yorker.
Rebecca Hersher and Allison Aubrey covered this story for NPR.
Carbon Brief has an in-depth summary of the report.
Here’s the executive director of Project Drawdown on how changing our land use and farming patterns can make a dent in addressing climate change.
The Trump administration announced plans to significantly weaken the Endangered Species Act, the US’s bedrock conservation law. By Lisa Friedman in NYT.
A Quarter of Humanity Faces Looming Water Crises. Somini Sengupta reports in NYT.
Alan Alda in conversation with climate scientist Katherine Hayhoe
How cheap does energy storage have to get before it can enable a 100% renewable energy system? By David Roberts in Vox.
What Worries Iceland? A World Without Ice. By Liz Alderman in NYT.
At least 60 people have been killed and over 200 thousand have been displaced by floods in the Indian state of Kerala. Muhammed Sabith reports in The Wire. This comes only a year after the previous monsoon’s extreme rainfall caused floods in Kerala.
Iceland is creating a memorial to a lost glacier. “Okjökull—a once-iconic glacier that has melted away throughout the 20th century and was declared dead in 2014.”
Excellent visualization of the inequalities in urban temperatures, mapped in five US cities. By Nadja Popovich and Christopher Flavelle in NYT.
“new research shows that temperatures on a scorching summer day can vary as much as 20 degrees across different parts of the same city, with poor or minority neighborhoods often bearing the brunt of that heat.”
Is eating seafood climate-friendly? It’s complicated. Informative video by Eve Andrews and Daniel Penner in Grist.
India plans to cut coal imports by a third. At the same time, it plans to increase domestic coal production, and is in talks to build coal mines in Australia.
Climate change made European heatwave up to 3°C hotter. By Quirin Schiermeier in Nature News.
Ulaanbaatar, Mongolia — the coldest capital city on Earth — also has one of the world’s worst cases of wintertime air pollution. Emily Kwong reports for NPR.
Hawaii’s snails are disappearing at a faster rate than any animal on Earth. A short documentary in The Atlantic. For more, read Ed Yong’s piece in the Atlantic, The Last of Its Kind.
That’s all for this week. See you next time!




